Importanța matematicii în viața de zi cu zi
Încă din antichitate, matematica a fost o parte integrantă a vieții noastre de zi cu zi.
Înțelegerea noastră despre matematică și dorința constantă de a extinde amploarea cunoștințelor noastre despre lume ne-au dus departe, astfel încât astăzi lumea așa cum o știm nu ar fi posibilă fără matematică.
Matematica este o aplicație a materiei și contribuie la toate comportamentele noastre metodice și sistematice. Matematica, de exemplu, a adus ordine în comunitățile de pe această planetă și a prevenit haosul și catastrofele. Multe dintre calitățile noastre umane moștenite sunt hrănite și dezvoltate de teoriile matematice, cum ar fi conștientizarea noastră spațială, abilitățile noastre de rezolvare a problemelor, puterea noastră de a raționa (care implică o gândire calculată) și chiar creativitatea și comunicarea.
Lucrurile la care nu te-ai aștepta să aibă vreo legătură cu matematica se rezumă, de fapt, la o nevoie fundamentală de matematică și la structura pe care aceasta o aduce în viața noastră de zi cu zi.
În plus, matematica este mereu prezentă în orice meserie sau profesie - indiferent dacă ești artist sau om de știință.
Un pictor își va folosi creativitatea combinată cu conștientizarea tuturor lucrurilor aflate direct în fața lui, precum și a lucrurilor din jurul lui. El va planifica (conștient sau nu) și va calcula, cu fiecare lovitură de pensulă, lungimea și impactul semnului pe care îl pune pe acea pânză, modul în care aceasta se raportează la restul piesei și modul în care se interconectează cu mediul mai larg al artistului.
Adăugă la asta faptul că va avea nevoie de buget pentru lucruri precum rechizite, unelte, studiouri etc. și, în plus, ar putea avea nevoie să-și folosească gândirea logică și cifrele pentru a stabili prețuri potrivite pentru opera sa de artă.
Și mai clar este faptul că un om de știință va fi în contact direct cu numere, măsurători, ecuații și formule în sarcinile de zi cu zi, iar matematica va domnii peste toate cercetările pe care le face.
Stai, totul sună puțin profund și destul de descurajant, nu-i așa? Să spui că matematica guvernează aproape totul în această lume și că importanța ei pentru viață este nemăsurată? Nu-ți face griji, aici vine partea distractivă!
Transformarea problemelor de matematică în beneficii
Matematica are o reputație în multe lucruri, de obicei cei care întâmpină dificultăți atunci când se confruntă cu ea, ca fiind o materie plictisitoare. Dar chiar nu este cazul! În plus, prin introducerea unor elemente distractive în modul în care elevilor le este predat teorii și concepte matematice, ar putea ajuta mult mai mulți elevi să exceleze în acest domeniu!
Este atât de ușor să nu vrem să reținem atunci când nu suntem atât de interesați. Dar, modalitatea prin care putem să reținem și procesăm informațiile importante și de a nu le lăsa să „ intre pe o ureche și să iasă pe cealaltă” este să ne bucurăm de rezolvarea lucrurilor.
Știai că te poți distra mult în timp ce înveți matematica și numeroasele trucuri și puzzle-uri pe care le prezintă? Mulți dintre noi nu putem rezista unei ghicitori bune, iar rezolvarea unor puzzle-uri logice dificile este un mod fantastic de a face asta.
A lucra la subiecte precum algebră, fracții și probabilitate poate fi mult mai distractiv decât ai crede! Dacă nu ne crezi, atunci încearcă aceste puzzle-uri interesante de matematică!
Așa e, este posibil să exersezi matematica în timp ce te distrezi! Fie că este o iluzie optică, un puzzle cu imagini sau jocuri de logică, găsirea răspunsului la un puzzle complicat este o modalitate excelentă de a te îmbunătății la rezolvarea problemelor.


Testează abilitățile analitice în matematică cu un puzzle complicat!
În încercarea de a înțelege lumea din jurul său, omul a folosit matematica în efortul de a obține dovezi tangibile. Istoria matematicii este punctată de minți mari care se luptă cu marile enigme ale timpului lor.
Puzzle-urile matematice combină raționamentul cu numerele, calculele și cifrele.
Pentru a rezolva astfel de puzzle-uri, nu trebuie să ai creierul unui geniu matematic, dar este important să adoptăm o abordare logică și să aplici abilitățile de matematică pe care le-ai învățat pe parcursul școlii, de la înmulțire și împărțire simplă, ecuații pătratice și calcul.
Așa că pregătește-te să-ți canalizezi matematicianul interior cu aceste 5 puzzle-uri provocatoare care pot fi întâlnite la orele de matematică.
Dar mai întâi!
Să ne gândim cum și de ce ne sunt atât de utile aceste puzzle-uri.
Beneficiile jocurilor de gândire pentru matematică
Nu totul este în capul tău! Antrenamentul creierului este la fel de bun pentru întregul tău corp cât și pentru bunăstarea ta.
NHS însuși afirmă că „menținerea minții active poate avea diverse beneficii, inclusiv un risc redus de demență. În general, ar părea rezonabil să menținem atât mintea, cât și corpul activi”.
Există diverse lucruri pe care le poate face pentru tine menținerea minții active cu antrenamentul cognitiv, cum ar fi:
- Creșterea capacității de memorare
- Reducerea riscului și încetinirii declinul bolilor mintale precum demența
- Îmbunătățirea vitezei de procesare a creierului
- Prevenirea plictiselii
- Îmbunătățirea concentrării
De asemenea, te-ai gândit vreodată la faptul că totul îți schimbă creierul? Fiecare persoană nouă pe care o întâlnești, fiecare poveste nouă pe care o citești, fiecare floare nouă pe care o miroși… există atât de multe „primuri” care continuă să aibă loc de-a lungul vieții noastre, la care probabil nici măcar nu ne gândim. Cu toate acestea, atunci când stai pe spate și te gândești la asta, creierul tău se dezvoltă constant și este influențat de mediul înconjurător.
Deci, dacă încă mai ai îndoieli cu privire la modul în care un pic de antrenament al creierului te poate ajuta, atunci gândește-te la asta: dacă, la fel ca multe altele, o singură imagine a unei celebrități care arată ideea ta de perfecțiune poate declanșa un puternic sentiment de motivație de a merge la sală/de a cumpăra niște haine noi/de a schimba felul în care îți faci părul etc, atunci nu poate un mic joc de matematică să aibă și forța să-ți schimbe mentalitatea? Cine știe ce ar putea face antrenamentul obișnuit al creierului în sensul cum abordezi matematica și cum gândești lucrurile în general!
Iată o formulă care se poate aplica dacă intenționezi să înveți matematică.
Matematică = Control = Auto-îmbunătățire = Satisfacție
Întrebări care stârnesc o gândire critică: Problema celor 100 de prizonieri
Sunt 100 de prizonieri, condamnați la moarte, într-o închisoare. Din senin, directorul închisorii propune o provocare.
El atribuie fiecărui deținut un număr între 1 și 100, apoi instalează în biroul său un dulap cu 100 de sertare, fiecare conținând un număr aleator între 1 și 100, corespunzător celor atribuite deținuților.
Fiecare număr apare o singură dată.
El cere fiecărui prizonier să deschidă 50 de sertare și să verifice numărul din fiecare.
Odată ce fiecare prizonier a intrat în birou, îi este interzis să comunice cu alți deținuți, nici să schimbe succesiunea extragerii sau să lase vreun indiciu.
Niciun prizonier nu va ști ce numere au văzut ceilalți deținuți.
Directorul închisorii oferă două rezultate posibile:
- Toți prizonierii își găsesc numărul respectiv și toți sunt grațiați.
- Nimeni nu își găsește numărul și toți sunt executați.
Care este șansa ca fiecare prizonier să găsească sertarul corespunzător numărului său?
Conform legii probabilității matematice, șansa ca toți să fie iertați este (1/2)100, sau 0.0000000000000000000000000000008.
Există o strategie inteligentă care oferă prizonierilor posibilitatea de a crește aceste șanse și de a trăi. Care este aceea?
Găsește un meditator de matematică în București la Superprof!
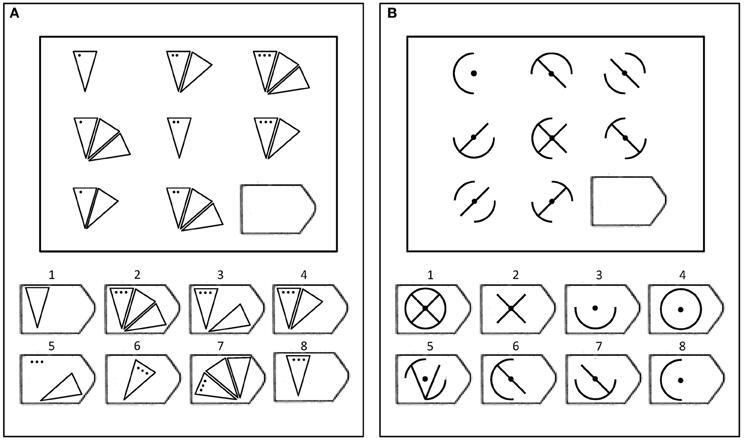
(Sursa: Frontiers in Psychology - Daniel Little et. al.)
Cei 3 Zei
În spatele a trei personaje numite A, B și C se ascund 3 zei cunoscuți ca „adevărat”, „fals” și „aleatoriu”.
Zeul „adevărat” răspunde întotdeauna cu adevărul, zeul „fals” mereu minte, iar cel „aleatoriu” alternează imprevizibil între cei doi.
Provocarea este „simplă”!: Descoperă identitățile respective ale lui A, B și C punând doar trei întrebări la care răspunsul este fie adevărat, fie fals.
Fiecare întrebare poate fi pusă doar unui zeu, dar dacă decideți să întrebați un singur zeu de mai multe ori (de maximum trei ori), ceilalți zei nu vor putea răspunde.
Întrebările tale pot să nu aibă legătură între ele.
Tortul Triunghiular
Când își pregătește clasa pentru un concurs de matematică, un profesor decide să ofere elevilor săi un tort sub forma unui triunghi cu trei laturi inegale.
Plasează o comandă la o cofetărie, dând măsurătorile celor trei laturi ale tortului.
Brutarul comandă o cutie pentru tort, dând aceleași măsurători. Când tortul este gata, însă, constată că, în timp ce măsurătorile au fost respectate, forma este mai degrabă simetrică decât identică cu cea a prăjiturii sale.
Îl cheamă pe profesorul de matematică pentru a-l întreba cum ar trebui să taie tortul astfel încât să încapă în cutie.
Profesorul răspunde că două tăieturi vor fi suficiente.
Cum ar trebui făcute acestea?
Problema pisicii și șoarecilor
O pisică și un șoarece decid să joace „cap sau pajură”.
Pentru a anima jocul, ei decid să schimbe regulile: fiecare jucător trebuie să aleagă o combinație de 3 rezultate (de exemplu, cap, coadă, cap).
Ei aruncă moneda de mai multe ori, iar primul care vede una dintre combinațiile sale apare în trei aruncări consecutive de monede câștigă jocul.
Cei doi jucători nu pot alege aceeași combinație.
Pisica, simțindu-se a fi jucătorul mai puternic, începe prima. Șoarecele, cel mai deștept dintre cei doi, decide să-l lase să meargă înainte.
Cum poate fi crescută șansa de câștig, pentru fiecare jucător?
Rața și Pisica
Există o rață în mijlocul unui iaz circular. La marginea acestui iaz se află o pisică nerăbdătoare.
În timp ce rața ar dori să guste din iarba de la marginea iazului, pisica și-ar dori foarte mult să guste in rață!
Pisica nu știe să înoate și îi este prea frică de apă pentru a intra în iaz.
Rața, între timp, are aripile prea mici pentru a putea zbura.
Știind că pisica poate alerga de patru ori mai repede decât poate înota rața, este posibil ca rața să ajungă la marginea iazului fără să fie prinsă de pisică?
Uite mai multe jocuri în care să folosești un raționament matematic
Un joc mental este o întrebare al cărei răspuns ar trebui să fie distractiv. Desigur, nu toată lumea se bucură de jocurile mentale – ba chiar pot fi frustrante, dar, odată ce le înțelegi, și tu le vei găsi amuzante.
Există toate tipurile de jocuri mentale; unele care implică condiții sau situații; altele bazate pe o anumită succesiune. De exemplu:
Tatăl lui Mary are cinci fiice: Nana, Nene, Nini și Nono. Care este numele celei de-a cincea fiice?
Unii s-ar putea să urmeze tiparul vocalelor și să proclame Nunu a fi a cincea fiică, dar, așa cum este adesea cazul în jocurile mentale, răspunsul este în întrebare.
Dacă tatăl lui Mary are cinci fiice, atunci Mary trebuie să fie una dintre ele… nu?
Gândirea critică poate avea, de asemenea, multe astfel de răspunsuri evidente, dar uneori necesită mai mult timp de gândire. De exemplu:
Dacă trei păsări depun trei ouă în trei zile, câte ouă depune o pasăre într-o zi?
Răspunsul la acesta este ambiguu. Din punct de vedere matematic, o pasăre depune 1/3 dintr-un ou într-o zi. Cu toate acestea, deoarece nicio pasăre cunoscută de om nu poate depune doar o treime dintr-un ou, răspunsul logic este fie unul, fie niciunul.
Vezi la ce ne referim prin frustrant?
Caută profesori avansați de matematică la Superprof!

Problemele dificile ar trebui să fie adecvate nivelului; desigur, nu am dori să torturăm niciun elev de matematică cu puzzle-uri care necesită anumite cunoștințe ale funcțiilor algebrice superioare atunci când nu sunt în acel stadiu de învățare!
Probleme dificile pentru elevii de școală primară
- Sunt necesare câteva aunări: folosind doar 8 opturi, cum le puteți adăuga împreună pentru a egala 1000?
- Răspuns: 888+88+8+8+8 = 1000
- Mă gândesc la un număr din trei cifre. A doua cifră este de patru ori mai mare decât a treia, iar prima este de trei mai mică decât a doua.
- Răspuns: 141
- Care trei numere dau același rezultat indiferent dacă sunt adunate sau înmulțite împreună?
- Răspuns: 1, 2 și 3
- Liam a făcut luni patru bulgări de zăpadă. Marți a făcut nouă și miercuri, 14. Câți a făcut joi și vineri?
- Răspuns: măriți suma cu cinci în fiecare zi.
Probleme mentale mai dificile
- Cea mai ridicată temperatură înregistrată la Heathrow pe 1 ianuarie a fost de -1 grad. Pe 2 ianuarie erau 4 grade. Care a fost temperatura pe 3 ianuarie dacă temperatura medie în primele trei zile ale lunii ianuarie a fost de 2 grade?
- Răspuns: 3 grade
- Un vânzător de hot dog dorește să cumpere cantități egale de cârnați și chifle, dar chiflele vin în pachete de 10 și cârnați în pachete de 8. Câte pachete din fiecare ar trebui să cumpere vânzătorul pentru a-și atinge scopul?
- Răspuns: 10 pachete de cârnați și opt pachete de chifle.
- Toate aceste afirmații sunt adevărate: AxB=12; A+B+C=12; şi B-A=1. Ce numere consecutive sunt reprezentate de A, B și C?
- Răspuns: A=3, B=4, C=5
Diferența dintre jocurile mentale dificile și ghicitori
Mulți oameni nu fac nicio distincție între aceste două tipuri de ghicitori ale minții. La urma urmei, ambele sunt întrebări menite să te facă să te gândești… nu?
Diferența dintre jocurile mentale și ghicitori constă în intenția lor.
O ghicitoare folosește uneori sensuri duble sau alte expresii care necesită ingeniozitate și gândire neliniară de rezolvat. Iată un exemplu excelent în acest sens:
Ce începe cu C, se termină cu C și are C în el? Un ceainic!
Pe de altă parte, un joc mental, în general, nu folosește o construcție dificilă sau sensuri multiple:
Sunt un număr impar. Dă la o parte o literă. Ce numar sunt?
Răspunsul, șapte, este de două ori adevărat: 7-1=6, care este un număr par, adăugat la faptul că eliminarea lui S lasă cuvântul par!
Jocurile mentale, în general au scopul de a te distra, deci sunt foarte eficiente ca o încălzire înainte de a-ți face lecțiile la matematică.
Dacă ești profesor, poți să salvezi câteva jocuri mentale pentru a-i liniștii pe elevii tăi când se simt prea stresați de la presiunea și dificultatea materiei.
Îngrijitori: și voi vă puteți cultiva cândirea prin a încerca ocazional câteva jocuri mentale.
Blocat în trafic? Aștepți la cabinetul medicului? Momentul perfect pentru a antrena mintea!

Logica puzzle-urilor în matematică
La fel ca puzzle-urile tradiționale ale căror piese interconectate formează o imagine completă, puzzle-urile logice îmbrățișează același principiu – minus piesele.
Puzzle-urile logice cer participantului să pună împreună acele piese figurative corect folosind doar procesele lor de gândire… și poate un creion pentru a nota.
Unele dintre cele mai populare puzzle-uri logice care implică numere includ Sudoku și KenKen. Un puzzle logic special care a impresionat toată planeta și a fost chiar o temă centrală a filmului de succes de la Hollywood „Căutarea fericirii” este…
Poți pune piesele împreună pentru a găsi răspunsul corect?

Cubul rubik, creația arhitectului Erno Rubik, a captivat lumea imediat după premiera sa în 1980. De atunci, mai multe forme au evoluat de la conceptul inițial cuboid: Rubik’s Snake și Rubik’s Magic, precum și o serie de puzzle-uri personalizate și chiar versiuni digitale.
Astăzi, la aproape 40 de ani de la debutul cubului, țările din întreaga lume găzduiesc competiții de speed-cubing. Unele dintre provocări implică rezolvarea cubului legat la ochi, rezolvarea cubului cu picioarele și, bineînțeles, rezolvarea puzzle-urilor în cel mai scurt timp. World Cubing Association reglementează și sponsorizează aceste evenimente.
Domnul Rubik a conceput puzzle-ul cub ca o provocare pentru studenții săi – era profesor de arhitectură la acea vreme.
Dispozitivul, realizat din lemn și ținut împreună de benzi de cauciuc, a fost menit să ofere elevilor săi experiență practică în manipularea unui obiect tridimensional.
Nu intenționase să creeze un puzzle de logică și, într-adevăr, nu știa că acesta era unul până când a încercat să-l readucă la starea inițială - toate culorile pe laturile lor respective.
Așadar, dacă ai timp liber și ai chef să faci ceva interesant, ridică un cub Rubik și vezi dacă poți concepe un nou algoritm pentru a-l rezolva!
Între timp, iată câteva alte puzzle-uri logice la care să-ți pui mintea la contribuție. Din păcate, nu sunt genul pe care îl poți manipula fizic!
- Ai o pungă care conține 10 mere. Întâlnești 10 prieteni, fiecare care își dorește un măr. Împărțiți merele – câte unul fiecărui prieten și mai aveți câte unul în pungă. Cum poate fi asta?
- Răspuns: i-ai dat ultimul prieten punga care conține ultimul măr.
- Ai trei pungi mici, fiecare conținând două bile. Geanta 1 are două bile albastre, geanta 2 are două bile verzi și geanta 3 are una verde și una albastră. Atingând mâna într-o singură pungă, extragi o marmură albastră; cât de probabil este ca marmura rămasă în acel sac să fie albastră?
- Răspuns: există o probabilitate de 2/3 ca și marmura rămasă să fie albastră.
- Cum poți adăuga două numere din 3 cifre pentru a fi întotdeauna egale cu 1089?
- Răspuns: alege un număr din 3 cifre și apoi inversează-l. Scade numărul inițial din numărul inversat și inversează rezultatul. Adaugă acel număr la rezultatul scăderii pentru a obține 1089
- Un cub solid de lemn de 4 inch este vopsit în roșu pe toate cele 6 laturi. Și apoi, este tăiat în cuburi de 1 inch. Câte dintre acele cuburi vor avea 3 laturi roșii, câte vor avea 2 laturi roșii sau 1 latură roșie și câte nu vor avea roșu deloc?
- Răspuns: 8 cuburi vor avea 3 laturi roșii, 24 vor avea 2 laturi roșii, 24 vor avea 1 latură roșie și 8 nu vor avea deloc roșii.
Unele dintre aceste puzzle-uri par să sfideze logica, ca în cazul nr. 2: cum poate cineva să aibă o probabilitate de 2/3 ca a doua bilă să fie albastră dacă bilele verzi depășesc numărul albastru după prima tragere?
Acest fenomen este cunoscut sub numele de problema Monte Hall și se bazează pe intuiție și eliminare.
Deoarece numărul total de bile din care să selectezi este de 3 și două dintre ele sunt albastre, ai șanse de 2 în 3 să selectezi din nou albastru.
1.Poți elimina punga care conține doar bilele verzi; evident că nu ai ales din ea. Rămân 2 pungi, fiecare conținând o bilă albastră.
2.Acum că ai eliminat (la figurat) 2 bile verzi, numărul de bile albastre rămase în pungi este dublu față de numărul de bile verzi…
3. Deoarece numărul total de bile din care să selectezi este de 3 și 2 dintre ele sunt albastre, ai șanse de 2 în 3 să selectezi din nou albastru.
Cei mai mulți spun că ai avea 50% șanse să alegi din nou albastru, dar, acum că am făcut calculele, vedem că presupunerea nu este corectă!
La fel și cu acel cub vopsit în roșu. Mulți par să presupună că este gol și neglijează să adauge cele opt cuburi nevopsite care alcătuiesc miezul cubului mai mare.
Punga cu mere și prietenii lacomi: mulți se gândesc că fiecare măr va fi scos din pungă pentru a fi dat, dar asta este necesar doar pentru primele nouă mere.
Lasă-l pe al zecelea prieten lacom să arunce punga cu mere pentru tine!
Cât despre cele trei cifre însumând întotdeauna 1089? De fapt, este destul de interesant să vezi cât de distractiv poate fi cu adevărat jocul cu algebra…
Caută profesori buni de matematică la Superprof!
Bonus: Trei ghicitori de matematică
Dacă îți plac jocurile distractive de matematică, jocuril de cuvintele, mah-jong sau jocurile mentale, îți vor plăcea aceste puzzle-uri:
#1

#2

#3

Rezultat = prima cifră * prima cifră, a treia cifră * a treia cifră
398 = 964 (33 88)
118 = 164 (11 88)
356 = 936 (33 66)
423 = 169 (44 33)
(Sursa: brainfans.com)
Omul și misterul
Omul a căutat întotdeauna să înțeleagă lumea în care a evoluat.
A cercetat fără a înceta, a consultat nenumărate volume și a dezbătut contemporanii săi, pentru a înțelege mai bine lumea matematicii. Fiecare răspuns a dus la mai multe întrebări.
Dorința de a rezolva ghicitori face parte din moștenirea noastră genetică: ne-am născut pentru a căuta răspunsuri.
De ce suntem aici, pe Pământ? Există viață după moarte? Care au fost primii oameni? Cum au trăit?
Încă din antichitate, unele dintre marile mistere înrădăcinate în matematică și fizică au fost foarte greu de înțeles :
- Cum au fost construite piramidele Egiptului; în ce scop au fost astfel aranjate?
- Cum putem explica geniul matematic al unor oameni mari precum Leonardo da Vinci, Arhimede, Newton, Henri Poincaré și Stephen Hawking?
- Alte mistere arheologice de importanță matematică care încă ne pun la încercare înțelegerea includ: Sfinxul din Egipt, stâlpul din Delhi; un stâlp de fier de peste 7 metri înălțime și vechi de 1600 de ani, care nu a ruginit niciodată, și Sferele Megalitice din Costa Rica; 300 de sfere fiecare cu diametrul de 2 metri și cântărind 16 tone, a căror perioadă de origine și scop rămân necunoscute.
Caută meditatori buni de matematică în Cluj la Superprof

Să te afunzi în problemele matematice poate fi o soluție bună să uiți de necazuri.
Pentru a face acest lucru, poate fi necesar să folosești:
- geometrie
- aritmetică mentală
- matematica aplicata
- diviziune lungă
- teoreme matematice
- trigonometrie
Puzzle-uri și lecții de matematică
Să iubești matematica… sau nu
Ar trebui să ne placă tuturor matematica și ecuațiile matematice?
De ce contează?
De ce unii oameni se plictisesc când vine vorba de acest subiect?
Care sunt câteva motive pentru a iubi rezolvarea problemelor de matematică?
- Matematica poate constata dacă ceva este fals sau adevărat.
- Există o anumită eleganță în teoriile matematice. Datorită conciziei și simplității lor, s-ar putea să descoperi că poți obține o nouă înțelegere doar cu o cantitate mică de studiu. Lucrul important este să cauți mereu să înțelegi, mai degrabă decât să înveți zeci de formule și teoreme fără să le înțelegi dedesubturile.
- Matematica poate fi foarte utilă în poker atunci când vine vorba de câștigarea unui pariu!
- Matematica este un instrument foarte puternic: este posibil să obținem rezultate excepționale și aplicații care la început par dincolo de înțelegerea noastră.
- Datorită matematicii, nu numai că vei dobândi o înțelegere mai profundă a lumii din jurul tău, dar vei fi mai capabil să abordezi alte discipline precum fizica, chimia și economia.
- Matematica este ca un joc prin faptul că este logic, formal și îți stimulează creierul la fel ca jocurile precum șahul, sudoku și chiar Candy Crush Saga!
- Odată ce ai înțeles principiile, matematica devine un fel de a doua natură care te ajută să înțelegi și să rezolvi problemele din jurul tău.
De ce mulți consideră matematica atât de dificilă?
- Matematica este propria sa limbă și, pentru a o folosi bine, trebuie să-i stăpânești gramatica, vocabularul și ortografia specifică .Există reguli de învățat și aplicat fără doar și poate.
- Ca subiect, necesită multă autodisciplină. Nu este suficient de bun să te mulțumești cu „aproape” la matematică: trebuie să fii concis și metodic.
Găsește meditatori buni de matematică la Superprof

- În cele din urmă, matematica este o disciplină solicitantă care necesită exersarea regulată și consecventă. Fie că ești singur în fața unui ecran, fie că citești din manual, fie că iei lecții cu un profesor privat de matematică, trebuie să fii muncitor și perseverent, mai ales în afara orelor tradiționale de matematică, dacă ești într-un astfel de program de studiu.
La ce te poți aștepta când studiezi la cursurile de matematică?
GCSE
Conform specificațiilor stabilite de guvern, un GCSE în matematică ar trebui să permită studenților să:
- să dezvolte cunoștințe, abilități și înțelegere fluente a metodelor matematice și
- concepte
- însuşirea, selectarea şi aplicarea tehnicilor matematice pentru rezolvarea problemelor
- raționați matematic, faceți deducții și inferențe și trageți concluzii
- să înțeleagă, să interpreteze și să comunice informații matematice într-o varietate de
- forme adecvate informaţiei şi contextului.
În timpul unui curs GCSE, subiectele principale pe care le veți întâlni în studiile dvs. de matematică sunt:
- Număr
- Algebră
- Raport, proporție și rate de schimbare
- Geometrie și măsuri
- Probabilitate
- Statistici
Cu siguranță există loc de distracție printre aceste module? Desigur, o mare parte depinde de profesorul tău și de stilul său de predare și de timpul pe care îl ai pentru a acoperi conținutul cu lecții, așa că nu-l pune în dificultate atunci când are o clasă care nu înțelegi totul rapid.
Acestea fiind spuse, nu este rău să întrebi dacă profesorul tău a auzit de aceste jocuri interesante de matematică și dacă ai putea să încerci niște puzzle-uri și jocuri similare în timpul orei!
Nivelul A
În ceea ce privește studenții A Level și AS, guvernul consideră că este important pentru ei să:
- să înțeleagă matematica și procesele matematice într-un mod care să promoveze încrederea, să favorizeze plăcerea și să ofere o bază solidă pentru progresul către studii ulterioare
- extinde gama lor de abilități și tehnici matematice
- înțeleagă coerența și progresul în matematică și modul în care sunt conectate diferite domenii ale matematicii
- aplice matematica în alte domenii de studiu și fi conștient de relevanța matematicii pentru lumea muncii și pentru situațiile din societate în general
- să-și folosească cunoștințele matematice pentru a lua decizii logice și raționate în rezolvarea problemelor atât în cadrul matematicii pure, cât și într-o varietate de contexte și să comunice clar rațiunea matematică a acestor decizii
- raționați logic și recunoașteți raționamentul incorect
- generalizează matematic
- construiască dovezi matematice
- să-și folosească abilitățile și tehnicile matematice pentru a rezolva probleme provocatoare care îi cer să decidă asupra strategiei de soluție
- recunoaște când matematica poate fi folosită pentru a analiza și rezolva o problemă în context
- reprezenta situații matematic și înțelege relația dintre problemele în context și modelele matematice care pot fi aplicate pentru a le soluționa
- desena diagrame și schițe grafice pentru a ajuta la explorarea situațiilor matematice și la interpretarea soluțiilor
- să facă deducții și să tragă concluzii folosind raționamentul matematic
- să interpreteze soluțiile și să comunice interpretarea lor în mod eficient în contextul problemei
- să citească și să înțeleagă argumentele matematice, inclusiv justificări ale metodelor și formulelor și să comunice înțelegerea lor
- să citească și să înțeleagă articole referitoare la aplicații ale matematicii și să comunice înțelegerea acestora
- utilizați eficient tehnologii precum calculatoarele și computerele și recunoașteți când o astfel de utilizare poate fi inadecvată
- își asumă o responsabilitate crescândă pentru propria învățare și evaluarea propriei dezvoltări matematice
Prin urmare, temele generale ale unui curs de matematică A-Level sunt următoarele, cu numeroase sub-subiecte alcătuind fiecare secțiune.
- argument matematic, limbaj și demonstrație
- rezolvarea problemelor matematice
- modelare matematică
Matematică la nivel de licență
La nivel de licență, poți alege să studiezi pentru o calificare de bază la matematică (nu mai puțin solicitant decât un curs mai specializat, vom adăuga noi!), dar poți alege să te concentrezi și pe o specialitate precum finanțe matematice, fizică matematică, biologie matematică, matematică actuală, istoria matematicii, relativitatea specială sau modulul cuantic, deși sunt disponibile multe statistici de specialitate, relativitate cuantică, medicală. în ultimii ani de licență în matematică.
Subiectele pe care le vei studia în timpul primul an de facultate pentru o licență de matematică includ:
- calcul
- algebră
- analiză
- mecanici
- probabilitate
- statistici
- geometrie
- vectori
- matematica computațională
Desigur, chiar dacă îți place matematica și crezi că ești destul de bun la asta (și cu siguranță o vei face după toate aceste jocuri de creier!), atunci nu trebuie să studiezi matematica, să zicem.
De ce să nu iei în considerare economia, ingineria, informatica, fizica sau fizica teoretică, sau altă materie de știință, cum ar fi chimia, biologia sau psihologia, ba chiar contabilitatea sau finanțele?
Unde te poate conduce matematica profesional?
Dacă ești în căutarea unei cariere în finanțe, atunci este necesar un anumit nivel de calificare la matematică, dar este posibil să nu ai neapărat nevoie de o diplomă. Domeniile pe care ai putea dori să le iei în considerare sunt contabilitatea, munca actuarială, gestionarea investițiilor, banking și retail banking.
În afară de sectorul financiar, există industrii precum inginerie și tehnologia informației care pot beneficia de cineva care se pricepe la cifre.
Alternative, diferite căi pe care le urmează absolvenții de matematică includ roluri precum ofițer de apărare și informații, statistician, cercetător operațional, matematician universitar, profesor de matematică într-o școală primară sau secundară sau poziții în domeniul dreptului, mass-media, afacerilor sau sectorului public.
Poți vedea ce locuri de muncă sunt disponibile pentru pasionații de matematică, vizitând un site web de locuri de muncă.
Până acum, sperăm te gândești la matematică ca la un subiect ce te poate ajuta să îți pui neuronii în mișcare! Deci, de ce să nu găsești un profesor online de matematică cu Superprof?
La fel de importante, ea ne oferă o mai bună înțelegere a lumii noastre.
Când știi unde să cauți, este ușor să vezi amprenta matematicii în viața noastră de zi cu zi!
Împărtășește cu noi ghicitorile și răspunsurile pe care le știi la matematică în comentarii!
Rezumă cu AI:














