Ceea ce știm este o picătură, ceea ce nu știm este un ocean.
Isaac Newton
În vastul univers matematic, formulele ocupă un loc central. Aceste ecuații celebre se găsesc în fiecare teoremă matematică din cele mai vechi timpuri până la descoperirile recente ale secolului al XX-lea. Cu fiecare nouă ecuație matematică vine un număr mare de întrebări noi și apar noi răspunsuri.
Următoarea este o antologie a unora dintre ecuațiile matematice care au schimbat modul în care vedem lumea.

Teorema lui Pitagora
Această teoremă care datează din 530 î.Hr., este probabil una dintre cele mai populare ecuații matematice care există.
Iată formula lui:
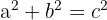
Teorema lui Pitagora este una dintre pietrele de temelie ale matematicii moderne și a contribuit semnificativ la dezvoltarea matematicii ca disciplină. Chiar și după mulți ani, formula acestei teoreme rămâne înrădăcinată în memoria noastră.
Într-un triunghi dreptunghic, pătratul ipotenuzei este egal cu suma pătratelor celorlalte două laturi.
Datorită lui Pitagora și a celebrei sale ecuații, putem calcula cu ușurință lungimi, unghiuri și putem determina dacă un triunghi este dreptunghic sau nu. Această ecuație este doar unul dintre numeroasele exemple ale modului în care matematica face parte din viața noastră de zi cu zi, indiferent dacă suntem conștienți de aceasta sau nu.
Teorema lui Pitagora continuă să fie folosită în domenii practice precum construcții, arhitectură și tâmplărie, printre altele.
Legea universală a gravitației
Legea universală a gravitației afirmă că două corpuri din univers se atrag unul pe altul cu o forță care depinde de masele lor și de distanța dintre ele.
Această forță este direct proporțională cu produsul maselor corpurilor și invers proporțională cu pătratul distanței dintre ele.
De exemplu, Pământul atrage Luna și invers.
Aceeași lege se aplică și atracției dintre un măr și Pământ și atracției dintre planete și Soare: Legea Universală a Gravitației.
Această lege și ecuație, una dintre cele mai faimoase ecuații matematice care există, a fost creată de Isaac Newton. El a formulat-o în secolul al XVII-lea. Formula este următoarea:
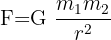
Unde:
- F: Forța gravitațională (N: Newtoni)
- M: Masa primului corp (de obicei o planetă, kg)
- m: masa celui de-al doilea corp (kg)
- R: distanța dintre corpuri (metri)
- G: Constanta gravitațională
Interacțiunea gravitațională este universală. Se aplică tuturor tipurilor de materie. Iar gravitația se manifestă doar ca atracție; nu ține cont de respingerea corpurilor.
Theory of Relativity
Matematica pură este, în felul său, poezia ideilor logice.
Albert Einstein
Formula pentru teoria relativității trebuie să fie una dintre cele mai faimoase ecuații care există. Și totuși, nimeni nu o înțelege pe deplin.
Teoria relativității a fost dezvoltată de Albert Einstein, care a ajutat la revoluționarea înțelegerii noastre științifice a naturii spațiului și timpului.
Această teorie este una dintre cele mai faimoase teorii matematice, iar formula sa este:
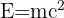
Dar la ce se referă această formulă?
În primul rând, este important de reținut că masa oricărui obiect este o formă de energie. În formulă, masa (𝑚) unui obiect poate fi convertită în energie (𝐸) și invers. „c” reprezintă viteza luminii și este clar faptul că până și o cantitate mică de masă poate fi transformată într-o cantitate mare de energie.
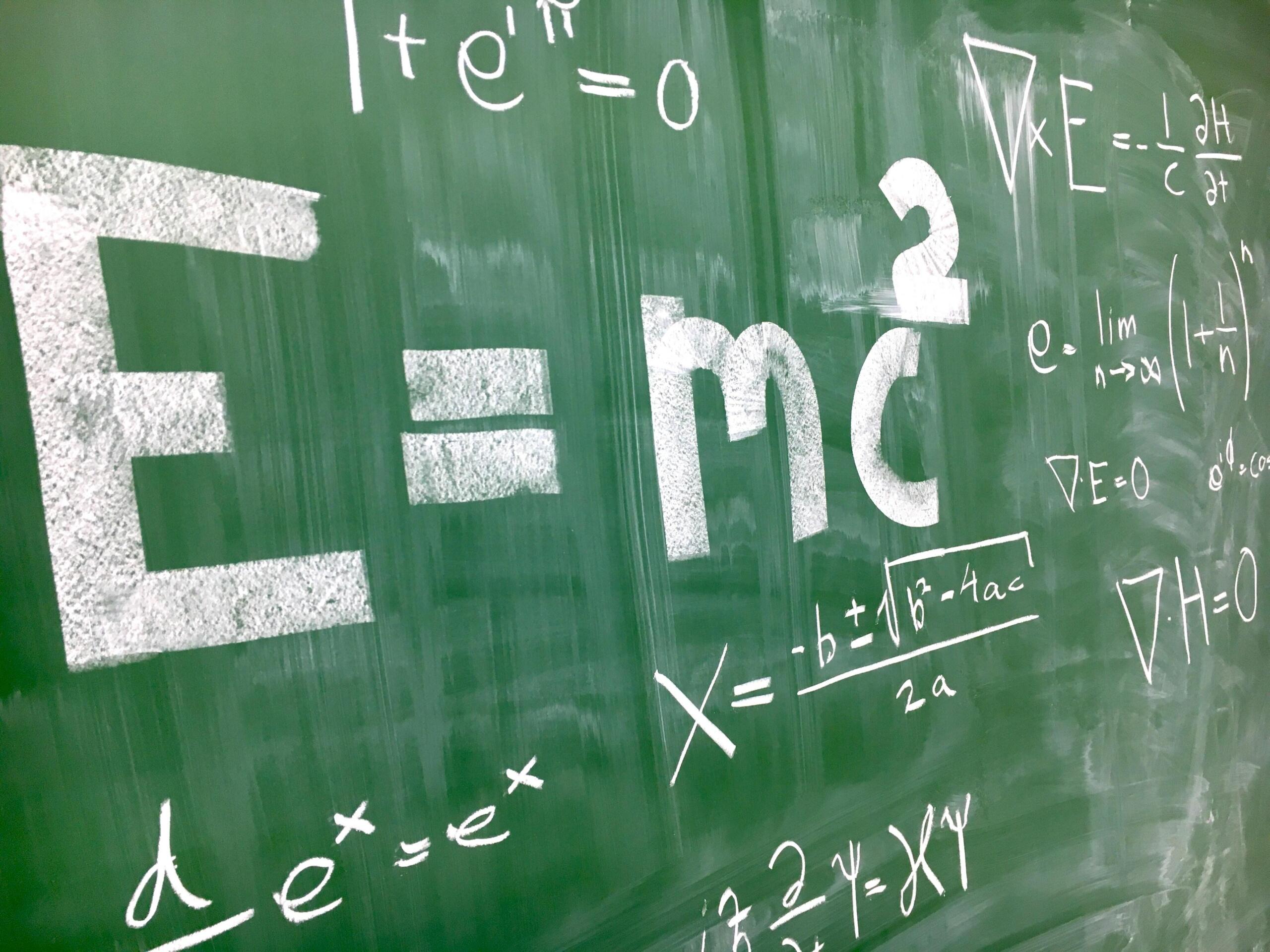
Această formulă, care ilustrează teoria relativității (relativitatea restrânsă și relativitatea generală) a revoluționat până în acel moment înțelegerea noastră asupra fizicii.
Rămâne crucial până în ziua de azi, deoarece arată că materia poate fi transformată în energie și invers 🤓
Relativitatea restrânsă a introdus ideea că viteza luminii era o constantă universală care nu se schimba și că trecerea timpului nu a fost aceeași pentru corpurile care se mișcă cu viteze diferite.
Teoria relativității este cea mai faimoasă teorie matematică din lume deoarece a demonstrat cât de importantă este matematica în viața reală și impactul principal pe care îl poate avea matematica în cursul istoriei.
Aria unui cerc

Un cerc este o curbă plată închisă în care toate punctele sunt echidistante de centru. În termeni simpli, un cerc este o linie închisă, ca un inel sau o anvelopă.
Formula sa este:
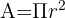
Unde
𝐴 este aria cercului.
Iar π (π = 3.1416)
și 𝑟, reprezintă raza cercului. Raza este distanța dintre centrul cercului și orice punct de pe limita acestuia.
Fie în scopuri practice, cum ar fi pictarea unei mese circulare, fie în fizică, aria unui cerc este esențială.
Datorită zonei cercului, am putut studia fenomenele ondulatorii, câmpurile electromagnetice, lentilele și chiar distribuția luminii în profunzime mai mare.

Teoria haosului
Teoria haosului este știința lucrurilor de neconceput, a neliniarului și a imprevizibilului. Este una dintre cele mai faimoase teorii matematice.
Această teorie se ocupă de fenomene neliniare care sunt practic imposibil de prezis sau controlat, cum ar fi turbulențele, vremea, bursele, stările creierului și multe altele. Aceste fenomene sunt adesea descrise folosind fracțiile matematice, care reflectă complexitatea infinită a naturii.
Teoria haosului cuprinde, de exemplu, efectul fluturelui .Acest efect este adesea descris după cum urmează: un fluture care bate din aripi în Australia poate provoca un uragan în Chile. Poate suna ca o fantezie, nu? Cu toate acestea, teoria haosului permite existența acestui efect. Mai exact, efectul fluturelui înseamnă că mici modificări ale condițiilor inițiale pot duce la modificări drastice ale rezultatelor.
Viețile noastre sunt o demonstrație constantă a acestui principiu. Deoarece nu putem cunoaște niciodată toate condițiile inițiale ale unui sistem complex până la cel mai mic detaliu, nu ne putem aștepta să prezicem rezultatul acestuia. Acest lucru ar putea fi în contradicție directă cu ideea ta de a folosi matematica pentru poker sau jocuri de noroc, deoarece chiar și erorile mici în măsurarea stării sistemului vor fi mult amplificate, făcând orice predicție inutilă. Aceasta este una dintre cele mai interesante teorii matematice.
Identitatea lui Euler
Identitatea lui Euler este dată de următoarea formulă:
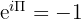
Mulți matematicieni și experți consideră că această ecuație este una dintre cele mai remarcabile ecuații create vreodată.
Nu este doar din cauza eleganței sale, ci și pentru că aceassta conectează cinci constante matematice importante într-o singură formulă:
- e: baza logaritmilor naturali
- i: constanta imaginară
- π: 3.1416
- 1 și 0: numere întregi
Eleganța identității lui Euler constă în simplitatea ei.
💡Datorită acestei simplități, a avut un impact semnificativ asupra domeniilor precum inginerie, teoria numerelor și funcții complexe, printre altele.
Identitatea lui Euler este egalitatea în care e este numărul lui Euler, baza logaritmilor naturali, i este unitatea imaginară, care satisface i2 = −1, iar π este pi, raportul dintre circumferința unui cerc și diametrul său.
A doua lege a termodinamicii
În timp ce prima lege a termodinamicii specifică faptul că energia poate fi schimbată între sistemele fizice sub formă de căldură și lucru mecanic. A doua lege introduce o altă mărime, cunoscută sub numele de entropie.
Este un principiu al schimbării și evoluției deoarece determină în ce direcție sunt posibile transformările de energie potențială.
Prin urmare, unele transformări chimice sunt posibile, în timp ce altele nu vor fi niciodată. Putem afirma cu siguranță, de exemplu, că dacă pui un cub de gheață într-o ceașcă de cafea fierbinte, cubul de gheață se va topi, în timp ce cafeaua nu va îngheța niciodată.
A doua lege a termodinamicii este un principiu fizic care impune o restricție asupra direcției proceselor de transfer de căldură între corpuri. A fost dezvoltată din generalizarea faptelor experimentale și a primit numeroase confirmări experimentale.
În termeni mai simpli, această lege spune că este imposibil ca un proces să aibă ca singur rezultat transferul de căldură de la un corp mai rece la unul mai fierbinte.
Deși mai mulți oameni de știință au contribuit la principiile acestei legi în trecut, popularitatea sa a fost atinsă în 1873 datorită lui Ludwig Boltzmann și Max Planck. Această lege introduce conceptul de entropie, care determină direcția în care au loc transformările de energie.
Să ne gândim la un cub de gheață pe care îl punem într-o ceașcă de ceai fierbinte.
Ce crezi că se va întâmpla?
Exact, gheața se va topi.
A doua lege a termodinamicii explică cum acest lucru se va întâmpla, și de ce nu invers: gheața NU va îngheța ceașca de ceai.
Ecuația Schrödinger
Această ecuație este una dintre cele mai faimoase formule din matematică. Nu, de data asta nu vorbim despre pisică; vorbim despre o altă idee genială a lui Schrödinger (Premiul Nobel pentru fizică).
Ecuația lui Schrödinger este esențială pentru înțelegerea modului în care particulele se schimbă în timp. Ne ajută să descriem diferitele stări în care poate fi găsită o particulă.
Dincolo de importanța sa tehnică, această ecuație ridică o întrebare filozofică fascinantă: Este materia într-adevăr compusă din stări fizice concrete, cum ar fi solide, lichide și gazoase, sau există ceva mai mult la mijloc? Cu alte cuvinte, ne invită să reflectăm asupra însăși naturii materiei și asupra modului în care o percepem. Acest tip de enigme matematice sunt foarte frecvente și această ecuație este o ușă către răspunsuri care vor fi găsite în cele din urmă.
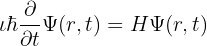
Ecuația lui Schrödinger a fost foarte utilă pentru dezvoltarea energiei nucleare, precum și pentru aplicații de calcul și laser.
Datorită acestei ecuații, una dintre cele mai faimoase ecuații matematice din istorie, am putut explica mai bine comportamentul atomilor și al particulelor subatomice.
Ecuația Schrödinger explică schimbările în timp ale unei particule. Descrie stările unei particule, din care este posibil să descriem orice stare.
Această ecuație ridică o adevărată întrebare filozofică: este materia alcătuită din prezența unor posibile stări fizice (solide, lichide, gazoase)?
Ecuațiile lui Maxwell
Cele patru ecuații ale lui Maxwell formează unul dintre cele mai importante fundamente ale fizicii moderne. Aceste ecuații au fost foarte semnificative atât pentru electrodinamică, cât și pentru teoria relativității.
Ecuațiile lui Maxwell arată cam așa:

Descoperirea ecuațiilor lui Maxwell este considerată punctul culminant al fizicii clasice, deoarece toate ecuațiile electromagnetismului pot fi derivate din ele. Aceste ecuații descriu interacțiunea dintre câmpurile electrice și magnetice și relația lor cu câmpurile și sarcinile electrice. Atât câmpurile electrice, cât și magnetice pot fi reprezentate folosind diagrame cu linii de câmp. Aceste ecuații au influențat cu siguranță importanța matematicii în lumea modernă, făcând evident că matematica este indispensabilă în societatea noastră.
Grafic vorbind, ambele reprezintă exercitarea unei forțe asupra sarcinilor. În termeni simpli, putem spune că aceste câmpuri electrice și magnetice sunt conectate. Ele interacționează între ele și pot fi modificate.
Aceste ecuații celebre au contribuit foarte mult în matematică. Ele nu sunt doar cunoștințe în sine, ci au permis și altor concepte matematice să fie create și rafinate.
Toate aceste ecuații matematice celebre au ceva în comun: sunt simple (din punct de vedere al eleganței), concise și ajută la conectarea matematicii fundamentale cu anumite concepte mai simple. Fiecare dintre aceste ecuații are aplicații extinse și profunde în viața de zi cu zi și în diverse discipline, lucru care le face foarte valoroase. Și deși matematica poate fi oarecum complexă, rămâne fascinantă.
Limbajul matematicii este universal. Nu contează dacă vorbești engleză, franceză sau spaniolă. Dacă înțelegeți limbajul matematicii, vei putea să te faci înțeles în orice limbă. Acest limbaj este conceput astfel încât să putem descoperi universul folosind o singură limbă, limbajul matematicii.
Sunt publicate în fiecare an!
Rezumă cu AI: